2018.增刊·专业成长·数学专场精彩课评

　　向数据的更深处漫溯

　　——听洪菲菲老师执教“平均数”一课有感

　　罗鸣亮

　　“平均数”是人教版四下的教学内容，它隶属于“统计与概率”的范畴。如今的教学，已经纠正了以往过于重视平均数的计算与应用而忽略其统计学意义的教学倾向，更加重视学生对平均数统计学意义的理解和掌握。在第四届“新课堂·新教师”海峡两岸基础教育交流研讨活动中，来自厦门的洪菲菲老师执教了“平均数”一课。听完她这节课，引发了笔者对平均数教学的诸多思考。

　　一、关于平均数，学生们已经知道了些什么

　　相较于其他统计量而言，平均数在日常生活中有着较为广泛的应用。例如，计算全班同学的平均成绩等。因此，学生们在进课堂前对平均数的认识不会是“白纸一张”，这点在洪老师的课堂上得到了印证。

　　【教学片段1】

　　课件出示男生队和女生队的投篮数(男生队：4个，6个，5个;女生队：3个，4个，7个，6个)。

　　师：同学们，请你们当小裁判。谁来说说到底是男生队成绩好呢，还是女生队成绩更棒?你是怎么判断的?

　　生：我觉得两支队伍打成平手。我们可以把男生队的总投篮数算出来，4+6+5=15，再把15除以3等于5，算出男生队的平均数。用同样的方法计算女生队的平均数，也是5。所以，男、女生两队的成绩相同。

　　师：哦，你说到了一个词“平均数”，你是怎么知道平均数的?

　　生：我们期末计算三科的平均成绩，就是把语文、数学、英语的成绩加起来，再除以3。

　　师：真棒，看来你对平均数有了一定的了解。这节课，我们进一步深入地了解一下平均数。

　　【赏析】在上述教学片段中，学生的“伶牙俐齿”给执教教师带来了一定的挑战。不难看出，学生对平均数已经有了较丰富的生活经验，甚至对平均数的计算方法也已经了然于胸。面对这种情况，教师该如何处理呢?是不是学生知道了平均数这个名词，懂得了平均数的计算方法之后，这节课的教学任务就已经完成，不需要再教学了吗?答案显然是否定的。学生已经了解了平均数的皮毛，如何在学生已有知识经验的基础上，带领学生向数据的更深处漫溯，揭开平均数的面纱，考验着教师的教学智慧。

　　二、关于平均数，我们要教什么

　　学生懂得了如何计算平均数，但对于为什么要学习平均数，平均数是怎么来的，却未必了然。也就是说他们处在“知其然而不知其所以然”的状态。如何引导学生认识平均数的本质呢?且看洪老师的精彩演绎。

　　【教学片段2】

　　师：刚才那位同学用计算的方法找到了平均数。请同学们看一看，还有什么方法也能找到男生队投篮的平均数。

　　生：可以把林炎投的1个球给文迪(如图1)，这样的话，3个男生的投篮数都变成了5，5就是男生队投篮的平均数。

　　师：同学们，像这样把多的补给少的，叫作“移多补少”。你们能不能用移多补少的方法，找一找女生队投篮的平均数呢?

　　……

　　师：我们班4个小队也分别进行了投篮活动，看看他们的投篮情况(如图2)。请同学们估一估，我们班平均每个小队投篮多少个?

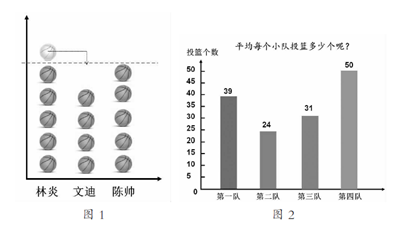
　　学生估，并上台指出平均数的位置。

　　师：刚才几位同学都估了平均数的位置。奇怪，为什么没有同学估50呢?为什么没有同学估24?

　　生：因为我们要把多的补给少的，要把第四队的投篮数补一些给投篮数少的队伍，所以这四个队投篮的平均数不可能是50;同样的道理，他们的平均数也不会是24。

　　师：看来，平均数不会是几个数据当中最大的那个数，也不会是最小的那个数，它应该在……

　　生：最大的数和最小的数之间。

　　师：那么，刚才几位同学估的平均数是对的吗?我们怎么判断?

　　生：用移多补少的方法验证一下。(课件演示)

　　师：当数据比较大的时候，用移多补少的方法难以找到平均数。有什么方法可以又快又准确地找到平均数呢?

　　生：可以用计算的方法。把4个小队的投篮数加起来，再除以4。也就是(39+24+31+50)÷4=36个。

　　师：这位同学用计算的方法找到了平均数。那么，36是不是这4个小队投篮的平均数呢?

　　生：用移多补少的方法验证一下。(课件演示)

　　师：看来，这位同学提出的计算的方法可行。我们是怎么计算出平均数的?

　　生：用总数除以份数等于平均数。

　　师：通过刚才的验证，我们发现了计算的过程其实也是移多补少的过程。

　　【赏析】在上述教学片段中，洪老师巧妙地引导学生体会了平均数“移多补少”的本质。首先，由学生观察数据特点，自行找到移多补少的方法。学生提出“将6个球中的1个移给4个球，这样3个男同学投篮的数量都成了5个，5就是男生队投篮的平均数”，这是学生对平均数“移多补少”本质的初体验。接着，洪老师创设了4个小队投篮的情境，并让学生估一估4个小队投篮的平均数。学生要完成估算的任务，就必须在脑海里主动完成“移多补少”的粗略过程，然后在统计图中找出平均数大致的位置。洪老师恰当地辅以课件演示，帮助学生验证所估平均数是否准确，这是对平均数“移多补少”本质的进一步认识和巩固。最后，教师启发学生思考：当数据较大时，移多补少不能很准确地找到平均数，有什么方法可以又快又准确地找到平均数呢?学生自然又想起了计算的方法。洪老师没有止步于此，而是继续引导学生用移多补少的方法验证计算出来的平均数，无痕地沟通了“先合后分”与“移多补少”之间的关系，使学生看到计算其实也是在移多补少。至此，学生完成了对平均数概念较为完整、准确的认知。

　　洪老师在平均数概念的教学中，力图在学生已有的认知基础上，引导学生探寻平均数“移多补少”的本质，并且阐明计算与移多补少之间的关系。平均数从一定意义上来说并不是“算出来”的，而是“移多补少”而来的。抓住了这一点，对于本节课教学目标的完成至关重要。

　　三、关于平均数的特点，我们要怎么教

　　要全面深入地认识平均数，我们还应当引导学生理解平均数的诸多特点。例如，平均数具有敏感性，数据的任何一点变化都会引起平均数的变化;平均数容易受到极端数据的影响;平均数总是介于最大值与最小值之间;一组数据中每一个数据与平均数之差的和等于0等。如何引导学生自然地理解平均数的这些特性呢?洪老师自有妙招。

　　【教学片段3】

　　师：我们班的“小百灵”笑笑参加学校的歌唱比赛，在初赛中她表现如何呢?我们看一看评委的打分情况。

　　课件出示：93，97，95，96，94。

　　师：这轮比赛笑笑的平均分是多少呢?

　　生：95分。

　　师：咦，你们怎么这么快就找到了这组数据的平均数呢?

　　生：把97移2分给93，把96移1分给94，就找到了它们的平均数95。

　　师：看来，对这组数据来说，用什么方法找平均数更简便?

　　生：移多补少。

　　师：笑笑在初赛中取得了95分的好成绩，那么，在决赛当中表现又如何呢?请看。

　　课件出示：96，95，94，97，73。

　　师：同学们，笑笑这轮比赛平均分还有95分吗?你觉得她的平均分可能是多少?

　　生：她这轮平均分会很低，可能达不到90分。

　　师：为什么呢，说说你的想法。

　　生：有一个评委打分特别低，只有73分。其他评委的分数要分一些给打73分的这位评委，所以平均分会被拉低。

　　师：是这样吗?同学们赶紧算一算，看平均分是不是被拉低了。

　　学生计算、汇报。

　　师：看来，你们的猜测是有道理的，这个特别低的分数确实拉低了比赛的平均分。如果有一位评委打分特别高，那么平均分会发生什么变化呢?

　　生：平均分会被拉高。

　　师：平均数容易受到特别大或者特别小的数据较大的影响。

　　师：请同学们想想，如果打73分的这位评委多打1分，笑笑在决赛中的平均分会发生变化吗?会发生怎样的变化?

　　生：平均分会升高一点点。因为多出来的1分还要平均分给5个评委，所以每位评委会分到0.2分，平均分应该会提高0.2分。

　　师：这位同学对平均数真有感觉。只是一个评委多打1分，平均分就发生了轻微的上升。难怪人们都说平均数很敏感，任何一点风吹草动都会引起平均数的变化。

　　【赏析】在上述教学片段中，洪老师通过有效的情境创设和精心设问，使学生感受到平均数的敏感性，以及容易受到极端数据影响的特点。从课堂教学来看，平均数的这些特性并不是教师“教”给学生的，而是学生自己悟出来的。学生感悟的源头在哪?其源头便在于前面学习的“移多补少”。因为深刻领会到平均数移多补少的本质，就抓住了学习的主线，顺着这条主线，学生自己体会到“平均数容易受到极端数据的影响”“平均数很敏感”等特点。再回溯之前的估平均数及验证平均数的教学过程，学生通过“移多补少”，也自然体悟到“平均数总是介于最大值与最小值之间”“超出平均数的部分补给不足平均数的部分刚刚好(即一组数据中各数据的离均差之和等于0)”的特性。平均数的这些特性，不需要教师刻意去设计教学、去组织学习，只要学生真正理解了平均数移多补少的本质，便能顺藤摸瓜，将平均数的诸多特性一一领悟。抓住了核心，把握住了本质，便起到了牵一发动全身的神奇效果。

　　不妨让我们再回到课的开始，学生娓娓道出平均数计算方法的那一时刻。是否因学生懂得了计算方法，这节课的教学就该戛然而止呢?学生认识的只是平均数的“冰山一角”，而洪老师准确地把握了教材，通过精心设计的各个教学环节，带着学生通过事实表面，真正理解了平均数的概念本质。当课堂教学中学生呈现出了“我会了”的表象时，教师不能简单认定为教学目标已经达成。好的教师应该在学生已有认知的基础上深入开掘，带着学生向知识的更深处漫溯，起到拨云见日、直达本质的教学效果。

　　(作者单位：福建省普通教育教学研究室　 责任编辑：王彬　黄哲斌)